Atobaum

Bézier curve

개요

평면 위의 유한한 곡선은 무엇일까? 정확하게 말하면 f:[0,1]→R2f: [0,1] \rightarrow \mathbb{R}^2 인 함수겠지만 매번 함수를 통해 말하기에는 피곤하다. 그래서 무수히 많은 곡선 중에 적당히 포기하고 몇개만 골라서 간단하게 표현하는 방법을 Paul de Casteljau란 사람이 만들었다고 한다. 그런데 우리는 이 곡선을 Bézier curve라고 부른다.

베지어 곡선은 몇개의 점으로 곡선을 표현한다.

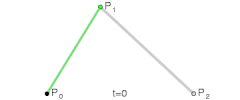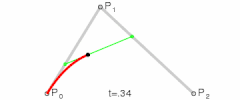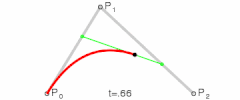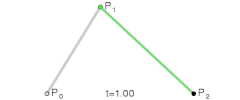
1차 베지어 곡선

P0,P1P_0, P_1가 평면 위의 점일 때 두 점을 잇는 직선은

f(t)=P0+t(P1−P0), t∈[0,1]f(t) = P_0+t(P_1-P_0),\ t \in [0, 1]

이다. f(0)=P0f(0)=P_0이고 f(1)=P1f(1)=P_1인 것을 알 수 있다. 그리고 tt가 0에서 1로 가면서 f(t)f(t)는 P0P_0에서 P1P_1로 이동한다.

linear curve

위의 식을 다르게 써보자:

BP0,P1(1)(t)=(1−t)P0+tP1, t∈[0,1]−(1)B_{P_0, P_1}^{(1)}(t) = (1-t)P_0+tP_1,\ t \in [0, 1] \quad - (1)

이때 위쪽 (n)은 n차 베지어 곡선이라는 말. 그런데 한 점에 가만히 있는 것도 하나의 곡선으로 볼 수 있다:

BP0(0)=P0, t∈[0,1]B_{P_0}^{(0)} = P_0,\ t\in[0,1]

이제 (1) 을 다시 써보자:

BP0,P1(t)(1)=(1−t)BP0(t)+tBP1(t), t∈[0,1]−(2)B_{P_0, P_1}(t)^{(1)} = (1-t)B_{P_0}(t)+tB_{P_1}(t),\ t \in [0, 1] \quad - (2)

재귀적 정의의 낌새가 보인다.

정의

n차 베지어 곡선은 n+1개의 점 P0,...,PnP_0, ..., P_n으로 다음과 같이 정의된다:

BP0(0)(t)=P0, t∈[0,1]BP0,P1,...,Pn(n)(t)=(1−t)BP0,...,Pn−1(t)+tBP1,...,Pn(t), t∈[0,1]ifn>0\begin{aligned} B_{P_0}^{(0)}(t) &= P_0,\ t\in[0,1] \\\\ B_{P_0,P_1,...,P_n}^{(n)}(t) &= (1-t)B_{P_0,...,P_{n-1}}(t)+tB_{P_1,...,P_n}(t),\ t\in[0,1] \qquad if \quad n > 0 \end{aligned}

(2)번 식에서 1차 베지어곡선이 0차 베지어 곡선(사실은 점이지만) 두개를 잘 이은 것처럼 n차 베지어 곡선은 n-1차 베지어 곡선 두개의 점을 잘 이은 곡선이다(...)

2차 베지어 곡선

그럼 2차 곡선은 어떻게 쓰여질까? 위의 식에 대입해보자

BP0,P1,P2B_{P_0, P_1, P_2}

BP0,P1,P2(2)(t)=(1−t)[(1−t)P0+tP1]+t[(1−t)P1+tP2]=(1−t)2P0+2t(1−t)P1+t2P2\begin{aligned} B_{P_0, P_1, P_2}^{(2)}(t) &= (1-t)[(1-t)P_0+tP_1] + t[(1-t)P_1+tP_2] \\\\ &= (1-t)^2 P_0 + 2t(1-t) P_1 + t^2P_2 \end{aligned}

3차 베지어 곡선

그럼 3차 곡선은?

Animation of a cubic Bézier curve, t in [0,1]

BP0,...,P3(3)(t)=(1−t)[(1−t)2P0+2t(1−t)P1+t2P2]+t[(1−t)2P1+2t(1−t)P2+t2P3]=(1−t)3P0+3(1−t)2tP1+3(1−t)t2P2+t3P3\begin{aligned} B_{P_0,..., P_3}^{(3)}(t) &= (1-t)[(1-t)^2 P_0 + 2t(1-t) P_1 + t^2P_2] + t[(1-t)^2 P_1 + 2t(1-t) P_2 + t^2P_3] \\\\ &=(1-t)^3P_0+3(1-t)^2tP_1+3(1-t)t^2P_2+t^3P_3 \end{aligned}

Explicit form

그럼 4차, 5차 곡선은? 아... 너무 귀찮다. 위의 식을 보다보면 계수가 어디선가 많이 본 거같다. 사실

BP0,...,Pn(n)(t)=∑i=0n(ni)(1−t)n−itiPiB_{P_0,...,P_n}^{(n)}(t) = \sum^n_{i=0} \binom{n}{i}(1-t)^{n-i}t^iP_i

이다. (ni)\binom{n}{i}는 binomial coefficient 또는 combination 또는 nCi_nC_i이다. 증명은 귀납법을 사용하면 되겠지만 여백이 너무 좁다. 심심하면 참고

어디에 쓸까?

Bézier씨는 자동차를 설계하는 데 사용했다고 한다. 우리는 CSS에서 transition을 설정할 때 timing function으로 사용할 수 있다:

transition-timing-function: cubic-bezier(0.25, 0.1, 0.25, 1);

파라미터들은 무엇일까? 타이밍 함수를 x축이 시간이고 y축이 위치인 함수로 이해할 수 있다. 어차피 여기서 저기까지 가는 방법을 기술하는 것이기 때문에 P0=(0,0),P3=(1,1)P_0=(0,0), P_3=(1,1)로 고정할 수 있다. 이제 필요한 파라미터는 P1P_1과 P2P_2의 x, y 좌표. 순서대로 P0P_0의 x, y좌표, P1P_1의 x, y좌표이다.

사실 ease, linear, ease-in 같은 것들도 다 특정한 2차 베지어 곡선의 별명이다.

반면 css에서 cubic-bezier()의 한계는 무엇일까? 3차 베지어 곡선은 3차 함수(wrt. t)이기 때문에 "왔다갔다"할 수 있지만 "왔다갔다왔다갔다" 이상은 할 수 없다.

cubic-bezier 사이트에 가서 parameter를 바꿔보면서 곡선을 구경해보자.

P.S. Bézier surfaces

그럼 곡선을 곡면으로 확장시킬 수도 있겠지? Bézier surfaces 참고

Reference